Curve Fitting from Raster Data
| URL | Description |
|---|---|
| Bezier Curve - Wikipedia | 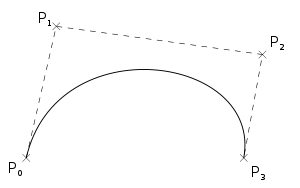 |
| Canvas Bézier Curve Example | |
| Cubic spline curves | A cubic spline curve is a piecewise cubic curve with continuous 2nd derivative. |
| Curve Fiting Using Bezier Splines (java example) | Created by Atanu Mohanty. More examples on the page below: Atanu Mohanty |
| Fitting B-Spline Curves to Point Clouds by Squared Distance Minimization |
|
| Fitting Polynomial Surfaces to Triangular Meshes... | Fitting Polynomial Surfaces to Triangular Meshes with Voronoi Squared Distance Minimization |
| Forcing Bezier Interpolation | A good description of how to find the Cube Bezier control points given 4 points on the curve. If P0...P3 are 4 points known on your curve, then y0...y3 are the control points that define the Bezier Curve.
[y0] = 1/27 * [ 27 0 0 0 ] * [ P0 ]
[y1] [ 8 12 6 1 ] [ P1 ]
[y2] [ 1 6 12 8 ] [ P2 ]
[y3] [ 0 0 0 27 ] [ P3 ]
|
| How to Draw Bezier Curves on an HTML5 Canvas | |
| How to approximate a vector contour from an elevation raster | |
| RasterToVector.com | |
| The Math Behind Bezier Cube Splines |
|